State abstraction is necessary for better task transfer in complex reinforcement learning environments. Inspired by the benefit of state abstraction in MAXQ and building upon hybrid planner-RL architectures, we propose RePReL, a hierarchical framework that leverages a relational planner to provide useful state abstractions.
Since the benefit of using the state abstractions is critical in relational settings, where the number and/or types of objects are not fixed apriori. We propose Dynamic-FOCI statements, an adaptation of first-order conditional influence (FOCI) statements, to specify the bisimilarity conditions of MDP. This helps us justify the safety of the abstractions. Additionally, since the RL agent learns to optimize policies to achieve subgoal with abstract state representations, we see effective transfer of learned skill from one task to another. In fact our experiments show that RePReL framework not only achieves better performance and efficient learning on the task at hand but also demonstrates better generalization to unseen tasks.
Motivational Example
In many real world domains, e.g., driving, the state space of offline planning is rather different from the state space of online execution. Planning typically occurs at the level of deciding the route, while online execution needs to take into account dynamic conditions such as locations of other cars and traffic lights. Indeed, the agent typically does not have access to the dynamic part of the state at the planning time, e.g., future locations of other cars, nor does it have the computational resources to plan an optimal policy in advance that works for all possible traffic events. We motivate this with a toy domain of an extended version of taxi domain where the goal is to transport multiple passengers ($p1, p2, p3, …$) to their respective destination location.
Here, the high level planning does not see the exact map of the domain, just plans for the passenger pick up and drop subgoals. While the lower level RL agent learns to navigate in the grid and accomplish these subgoals. In this setting, task specific abstraction can boost the sample efficiency tremendously. For e.g., the RL policy that is performing pickup $p1$ subgoal, needs to know the location of $p1$ and whether the taxi is free, while passenger $p2$ and destination of $p1$ are irrelevant.
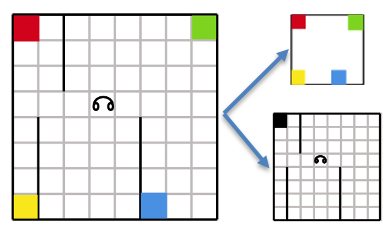
Abstract representations for Taxi domain with multiple passengers; high level planner doesn't see the whole map and lower level RL agent doesn't see other passenger locations
It has been argued that for human-level general intelligence, the ability to detect compositional structure in the domain (Lake, Salakhutdinov, and Tenenbaum 2015) and form task-specific abstractions (Konidaris 2019) are necessary. Our RePReL framework propose a step in that direction by providing the D-FOCI formulation which enables domain expert to specify the task specific abstract representation.
D-FOCI
Since states are conjunctions of literals in Relational MDPs, we need to reason about how the actions influence the state predicates and how rewards are influenced by goal predicates and actions to decide which literals should be included and excluded in the abstraction. We capture this knowledge using First-Order Conditional Influence (FOCI) statements (Natarajan et al. 2008), one of the many variants of statistical relational learning languages (Getoor and Taskar 2007; Raedt et al. 2016).
Each FOCI statement is of the form: “if $\text{condition}$ then $X1$ $\text{influence}$ $X2$”, where, $\text{condition}$ and $X1$ are a set of first-order literals and $X2$ is a single literal. It encodes the information that literal $X2$ is influenced only by the literals in $X1$ when the stated condition is satisfied.
For RePReL, we simplify the syntax and extend FOCI to dynamic FOCI (D-FOCI) statements. In addition to direct influences in the same time step, D-FOCI statements also describe the direct influences of the literals in the current time step on the literals in the next time step. To distinguish the two kinds of influences, we show a $+1$ on the arrow between the sets of literals to capture a temporal interaction, as shown below.
\[\text { operator }:\left\{\mathrm{p}\left(X_{1}\right), q\left(X_{1}\right)\right\} \stackrel{+1}{\longrightarrow} \mathrm{q}\left(X_{1}\right)\]It says that, for the given $\text{operator}$, the literal $q(X1)$ in the next time step is directly influenced only by the literals ${p(X1), q(X1)}$. Following the standard DBN representation of MDP, we allow action variables and the reward variables in the two sets of literals. To represent unconditional influences between state predicates, we skip the $\text{operator}$.
These D-FOCI statements can be viewed as relational versions of dynamic Bayesian networks (DBNs) and have a similar function of capturing the conditional independence relationships between domain predicates at different time steps. Hence, Q-learning with these abstractions result in an optimal policy for round MDP when the MDP satisfies the D-FOCI statements with fixed depth unrolling.
Experiments
Our evaluations try to answer three specific questions,
- Sample Efficiency: Do the abstractions induced by RePReL improve sample efficiency?
- Transfer: Do abstractions allow effective transfer across tasks?
- Generalization: Does RePReL efficiently generalize to varying number of objects?
All three are answered positively. Refer our ICAPS 2021 paper for more details on optimality guarantees, learning algorithm, evaluations, and results.
A sample implementation is available on our lab github here.
Citation
If you build on this code or the ideas of this paper, please use the following citation.
@inproceedings{KokelMNBT21,
title={RePReL: Integrating Relational Planning and Reinforcement Learning for Effective Abstraction},
author={Kokel, Harsha and Manoharan, Arjun and Natarajan, Sriraam and Balaraman, Ravindran and Tadepalli, Prasad},
booktitle={Thirty First International Conference on Automated Planning and Scheduling ({ICAPS})},
year={2021}.
url={https://ojs.aaai.org/index.php/ICAPS/article/view/16001},
}
Acknowledgements
HK & SN gratefully acknowledge the support of ARO award W911NF2010224. SN acknowledges AFOSR award FA9550-18-1-0462. PT acknowledges support of DARPA contract N66001-17-2-4030 and NSF grant IIS-1619433. AM gratefully acknowledge the travel grant from RBCDSAI. Any opinions, findings, conclusion or recommendations expressed in this material are those of the authors and do not necessarily reflect the view of the ARO, AFOSR, NSF, DARPA or the US government.