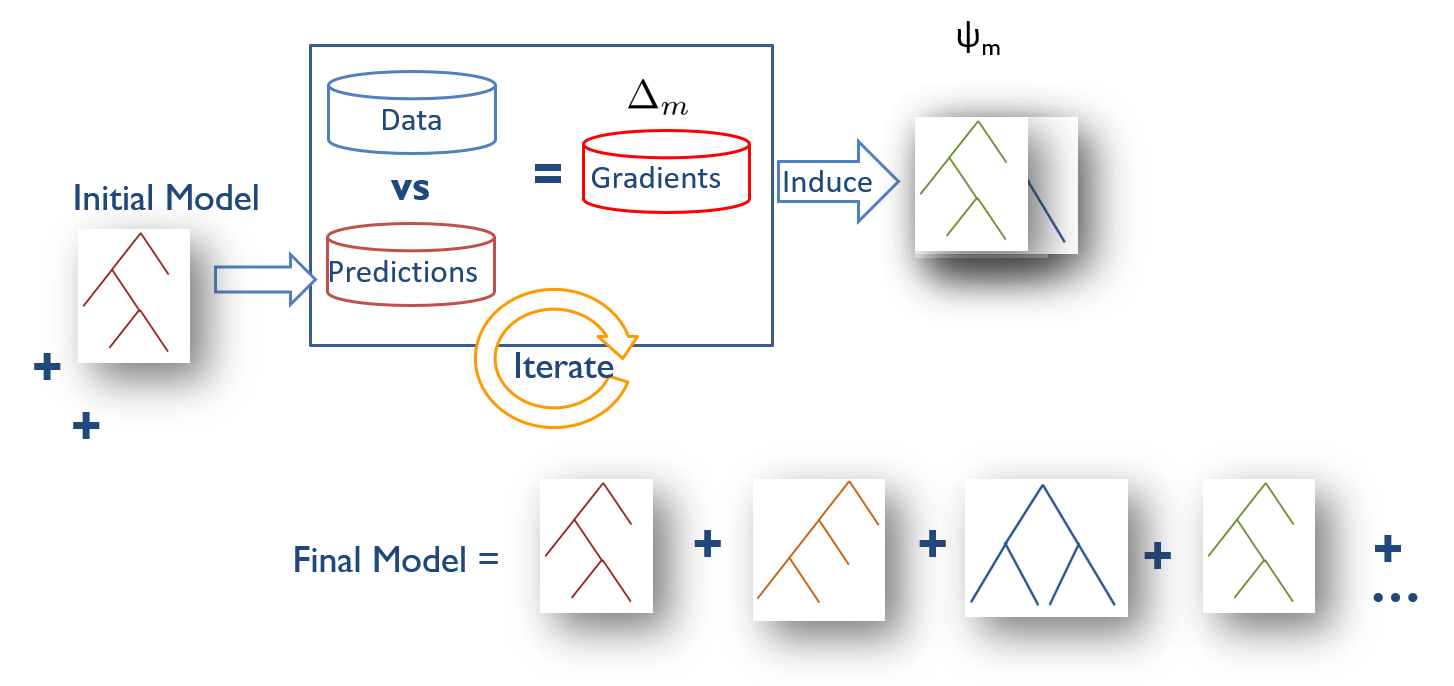
Boosting

Statistical Relational Learning models combine the representational power of first-order logic with the ability of probability theory to handle uncertainity. While these models are attractive from modelling perspective, learning them is computationally intensive. Existing approaches so far focused on the task of learning the so-called parameters where the rules are provided by the human expert and the data is merely used to learn the parameters. Our gradient boosted approach, instead relies on the intuition that learning a set of weak partial rules can be much easier than finding a single, highly accurate model. We learns both the rules and the parameters of the rules simultaneously. Our approach is capable of learning different types of models (Markov Logic Networks, Relational Dependency networks as well recently succesful Relational Logistic Regression), handling modeling of hidden data, learning with preferences from humans, scaling with large amounts of data by approximate counting and modeling temporal data.

Publications

• Sriraam Natarajan, Tushar Khot, Kristian Kersting, Bernd Gutmann and Jude Shavlik. “Boosting Relational Dependency Networks”, International Conference on Inductive Logic Programming (ILP) 2010.
• Tushar Khot, Sriraam Natarajan, Kristian Kersting, and Jude Shavlik. “Learning Markov Logic Networks via Functional Gradient Boosting”, International Conference in Data Mining (ICDM) 2011.
• Sriraam Natarajan, Saket Joshi, Prasad Tadepalli, Kristian Kersting, and Jude Shavlik. “Imitation Learning in Relational Domains: A Functional-Gradient Boosting Approach”, International Joint Conference in AI (IJCAI) 2011.
• Phillip Odom, Tushar Khot, Reid Porter, and Sriraam Natarajan, “Knowledge-Based Probabilistic Logic Learning”, Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI), 2015.
• Shuo Yang, Tushar Khot, Kristian Kersting and Sriraam Natarajan, “Learning Continuous-Time Bayesian Networks in Relational Domains: A Non-Parametric Approach”, 30th AAAI Conference on Artificial Intelligence (AAAI), 2016.
• Shuo Yang, Tushar Khot, Kristian Kersting, Gautam Kunapuli, Kris Hauser and Sriraam Natarajan, “Learning from Imbalanced Data in Relational Domains: A Soft Margin Approach”, International Conference on Data Mining (ICDM), 2014.
• Nandini Ramanan, Gautam Kunapuli, Tushar Khot, Bahare Fatemi, Seyed Mehran Kazemi, David Poole, Kristian Kersting and Sriraam Natarajan, “Structure Learning for Relational Logistic Regression : An Ensemble Approach”, International Conference on Principles of Knowledge Representation and Reasoning (KR), 2018.