Tree based gradient boosting methods are very powerful and are successfully used in various challenging problems. But they fail in region where data is absent or when majority of data is noisy.
In real-world problems, data is often sparse and noisy. So, can we leverage qualitative domain knowledge for regions where data is noisy or absent? Yes, our Knowledge-intensive gradient boosting approach provides a way to do that.
Given a sparse/noisy dataset, similar to the dataset shown in figure below, and some qualitative knowledge of the domain, KiGB learns boosted trees. The qualitative knowledge or trends of a domain can be expressed as monotonic influences. For the dataset below, monotonic influence $a_{ <}^{Q+}y$ indicated higher values of variable \(a\) stochastically results in higher values of variable $y$.

Dataset with X-Y axis represent features $a$ and $b$ resp.
and color/shape represent the target variable $y$
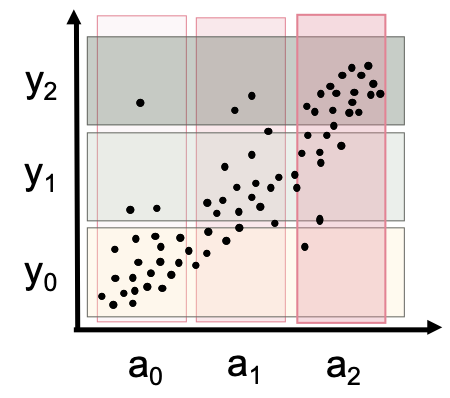
Monotonic influence of feature $a$ on target variable $y$
In order restricted statistics, monotonic influence implies following constraint: $a_1 < a_2 \implies \psi (a_1) \leq \psi (a_2)$, i.e. given $a_1$ is less than $a_2$ the value of $y=\psi(a_1)$ should also be less than $\psi(a_2)$
Altendorf et al. UAI, 2005 and Yang and Natarajan, ECML-PKDD, 2013 converts monotonic influences to constraints on probability distribution as: $a_1 < a_2 \implies P(Y\leq k \vert \boldsymbol{pa_{y}^{a_1}}) \geq P(Y\leq k \vert \boldsymbol{pa_{y}^{a_2}})$, i.e. given $a_1$ is less than $a_2$ the probability of $y$ less than any constant $k$ should be greater for $y$ given $a_1$ then $y$ given $a_2$ ceteris paribus.
We use a similar constraint for a tree, when a node split at variable with monotonicity constraint, the expectation of the left subtree should be less than that of right subtree. (Assuming that the split criteria is $\leq$)
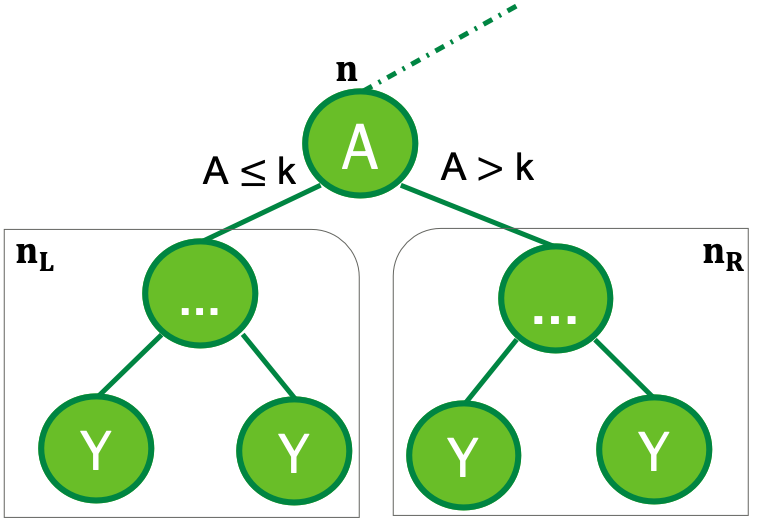
we obtain following constraint, which we name $\zeta$,
\[\mathbb E_{\psi}[\boldsymbol n_L] - \mathbb E_{\psi}[\boldsymbol n_R] - \varepsilon < 0, \quad \quad \quad \Bigg\} \zeta_n\]When $\zeta$ is greater than $0$ the constraint is violated. We modify the objective to include a loss function with $\zeta$,
\[\underset{\psi_{t}}{\operatorname{argmin}} \underbrace{\sum_{i=1}^{N}\left(\tilde{y}_{i}-\psi_{t}\left(x_{i}\right)\right)^{2}}_{\text {loss function w.r.t. data }}+\underbrace{\frac{\lambda}{2} \sum_{\mathbf{n} \in \mathcal{N}\left(\mathbf{x}_{c}\right)} \max \left(\zeta_{\mathbf{n}} \cdot\left|\zeta_{\mathbf{n}}\right|, 0\right)}_{\text {loss function w.r.t. advice }}\]Here, parameter $\lambda$ determines the importance of advice. Taking gradient of modified objective, we get a nice leaf update equation,
\[\psi_{t}^{\boldsymbol\ell}(\mathbf{x}) \, = \underbrace{\frac{1}{|\boldsymbol\ell |} \sum_{i = 1}^N \, \tilde{y}_i \cdot \mathbb{I}({x}_i \in {\boldsymbol\ell})}_\textrm{mean} + \\ \underbrace{\frac{\lambda}{2} \underset{\mathbf{n} \in \mathcal{N}(\mathbf{x}_c)}{\sum} \mathbb{I}(\zeta_\mathbf{n} > 0) \zeta_\mathbf{n} \cdot \Big( \frac{\mathbb{I}({\boldsymbol\ell} \in \mathbf{n}_\mathsf{R})}{ |\mathbf{n}_\mathsf{R}|} - \frac{\mathbb{I}({\boldsymbol\ell} \in \mathbf{n}_\mathsf{L})}{|\mathbf{n}_\mathsf{L}|} \Big)}_\textrm{penalty for advice violation}\]Notice that the penalty is directly proportional to the violation and inversely proportional to the number of data points. Thus, there is a trade-off between advice and data. Equilibrium can be obtained by tuning the hyperparameters – $\varepsilon$ and $\lambda$.

For more details on the empirical evaluations, background on other monotonicity based approaches, or gradient derivation refer our AAAI 2020 paper.
Code and the usage guide can be found here.
Citation
If you build on this code or the ideas of this paper, please use the following citation.
@inproceedings{kokelaaai20,
author = {Harsha Kokel and Phillip Odom and Shuo Yang and Sriraam Natarajan},
title = {A Unified Framework for Knowledge Intensive Gradient Boosting: Leveraging Human Experts for Noisy Sparse Domains},
booktitle = {AAAI},
year = {2020}
}
Acknowledgements
- Harsha Kokel and Sriraam Natarajan acknowledge the support of Turvo Inc. and CwC Program Contract W911NF-15-1-0461 with the US Defense Advanced Research Projects Agency (DARPA) and the Army Research Office (ARO).