Getting Started
Background
Prerequisites:
- programming experience is strongly recommended
- basic shell experience (moving between folders, viewing files)
- an Apple/Linux machine (Windows coming soon)
At its core, this is a brief “Inductive Logic Programming” (ILP) tutorial. However, we are learning probabilistic (weighted) clauses. Following any standard logic learner, we assume that the data is structured i.e., consists of objects and relationships between the objects. The goal is to induce a theory (regression trees with logical variables in them) from a set of examples (positive and negative as separate files), facts (values of the attributes and/or relationships) and some background knowledge, all in predicate logic format. More on the background knowledge later. Like a typical ILP learner, ours is a discriminative learner and hence requires both positive and negative examples.
Like many things in computer science, usually the best way to learn something is by doing it.
Download the data, a copy of the jar file, and the AUC jar and follow along!
unzip Father.zipmv v1.0.jar Father/BoostSRL.jarmv auc.jar Father/auc.jarcd Father
Setup as Tables
- Suppose we have data about some people and some of their relationships. (we’ll refer to this information as “facts,” more on that later)
| Name | Sex | Child | Sibling |
|---|---|---|---|
| James Potter | Male | [Harry Potter] | - |
| Lily Potter | Female | [Harry Potter] | - |
| Harry Potter | Male | - | - |
| Arthur Weasley | Male | [Ron, Fred, Ginny] | - |
| Molly Weasley | Female | [Ron, Fred, Ginny] | - |
| Ron | Male | - | [Fred, Ginny] |
| Fred | Male | - | [Ron, Ginny] |
| Ginny | Female | - | [Ron, Fred] |
Note that the Child and Sibling are multi-arity relations and hence can have sets of values instead of a single value.
- Assume that the goal is to learn father(X)?. This means that the goal is to learn logic rules for the father of any given domain object X (persons in this case), given the information in the tables, i.e. given that you know the names of the domain objects, their sex, their children and their siblings.
From Tables to First-order Predicate Logic Notation
Once we have the high-level idea of what these relationships look like, the next step is to convert this into predicate logic format. This is the standard format for most Prolog-based systems but based on feedback from the users of the previous version, we provide a more detailed tutorial on its construction. However, we recommend that a script be used for this automatic construction.
A key difference to standard Prolog systems is that our system makes a restrictive assumption - no function symbols. We only handle predicate (boolean) symbols for ease of learning. However, note that a n-valued function can be represented using n different binary predicates with a mutual exclusive constraint.
A few things to consider during the transition:
- ‘Name’ is an identifier.
- ‘Sex’ is assumed to be either male or female, so we can simplify by making it a True/False value.
- childof, siblingof, and fatherof are binary relations, i.e., they encode the relation between two people (e.g. childof(mrbennet,jane), denotes that Jane is the parent of Mr. Bennet)
The target we want to learn is father(x,y). To learn this rule, the algorithm learns a decision tree that most effectively splits the positive and negative examples. This example is fairly small, and hence a few trees should suffice. However, for more complex problems we need more trees to learn a robust model. In most of our experiments, we use at least 20 trees.
Positive Examples
father(harrypotter,jamespotter).
father(ginnyweasley,arthurweasley).
father(ronweasley,arthurweasley).
father(fredweasley,arthurweasley).
...
Negative Examples
father(harrypotter,mollyweasley).
father(georgeweasley,jamespotter).
father(harrypotter,arthurweasley).
father(harrypotter,lilypotter).
father(ginnyweasley,harrypotter).
father(mollyweasley,arthurweasley).
father(fredweasley,georgeweasley).
father(georgeweasley,fredweasley).
father(harrypotter,ronweasley).
father(georgeweasley,harrypotter).
father(mollyweasley,lilypotter).
...
Facts
male(jamespotter).
male(harrypotter).
male(arthurweasley).
male(ronweasley).
male(fredweasley).
male(georgeweasley).
siblingof(ronweasley,fredweasley).
siblingof(ronweasley,georgeweasley).
siblingof(ronweasley,ginnyweasley).
siblingof(fredweasley,ronweasley).
siblingof(fredweasley,georgeweasley).
siblingof(fredweasley,ginnyweasley).
siblingof(georgeweasley,ronweasley).
siblingof(georgeweasley,fredweasley).
siblingof(georgeweasley,ginnyweasley).
siblingof(ginnyweasley,ronweasley).
siblingof(ginnyweasley,fredweasley).
siblingof(ginnyweasley,georgeweasley).
childof(jamespotter,harrypotter).
childof(lilypotter,harrypotter).
childof(arthurweasley,ronweasley).
childof(mollyweasley,ronweasley).
childof(arthurweasley,fredweasley).
childof(mollyweasley,fredweasley).
childof(arthurweasley,georgeweasley).
childof(mollyweasley,georgeweasley).
childof(arthurweasley,ginnyweasley).
childof(mollyweasley,ginnyweasley).
...
Training a Model
There’s one more piece we need: the background.
background
// Parameters
setParam: maxTreeDepth=3.
setParam: nodeSize=1.
setParam: numOfClauses=8.
// Modes
mode: male(+name).
mode: childof(+name,+name).
mode: siblingof(+name,-name).
mode: father(+name,+name).
Enter the directory and run the jar file to train the model.
java -jar BoostSRL.jar -l -combine -train train/ -target father -trees 10
First it finds childof(B,A):
“fathers are parents”
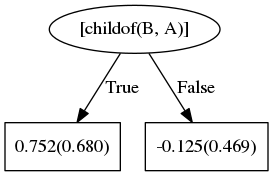
Next, if the person is male, they are also more likely to be a father:
“fathers are male”
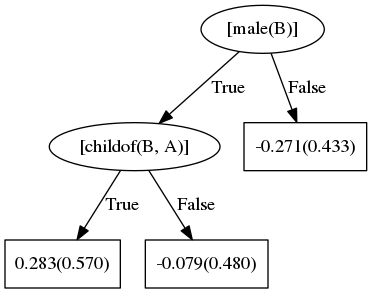
Each tree builds on the error of the previous tree. By combining the trees the model learned, we can see the decision the model finds most accurate.

This tree shows that a male father E is the parent of child D. Alternatively, the person is also the father to his child’s siblings.
Testing a Model
Technically we’re querying a model for an answer here, but we’ll call it the testing phase.
- We have a new set of data, and we want to know about the father(x) relationship:
| Name | Sex | Child | Sibling | Father |
|---|---|---|---|---|
| Mr. Bennet | Male | [Elizabeth, Jane] | - | ? |
| Mrs. Bennet | Female | [Elizabeth, Jane] | - | ? |
| Elizabeth | Female | - | [Jane] | ? |
| Jane | Female | [Elizabeth] | - | ? |
| Mr. Lucas | Male | [Charlotte] | - | ? |
| Mrs. Lucas | Female | [Charlotte] | - | ? |
| Charlotte | Female | - | - | ? |
- Outline the facts and “positive examples” to test:
Facts
male(mrbennet).
male(mrlucas).
male(darcy).
childof(mrbennet,elizabeth).
childof(mrsbennet,elizabeth).
childof(mrbennet,jane).
childof(mrsbennet,jane).
childof(mrlucas,charlotte).
childof(mrslucas,charlotte).
siblingof(jane,elizabeth).
siblingof(elizabeth,jane).
Positive Examples
In this case, we’ll only add the examples we want to test.
father(elizabeth,mrbennet).
father(jane,mrbennet).
father(charlotte,mrlucas).
father(charlotte,mrsbennet).
father(jane,mrlucas).
father(mrsbennet,mrbennet).
father(jane,elizabeth).
- Run the testing command from the
Fatherdirectory:
java -jar BoostSRL.jar -i -model train/models -test test/ -target father -aucJarPath . -trees 10
- Enter the
testdirectory and look at the results:
cd testless results_father.db
The results will look something like this:
father(elizabeth, mrbennet) 0.8469089683281722
father(jane, mrbennet) 0.8469089683281722
father(charlotte, mrlucas) 0.8469089683281722
father(charlotte, mrsbennet) 0.03200025741806517
father(jane, mrlucas) 0.06111079239086714
father(mrsbennet, mrbennet) 0.06111079239086714
father(jane, elizabeth) 0.03200025741806517
- Results in a nicer format:
| Person A | Person B | Probability of B being the father of A |
|---|---|---|
| Elizabeth | Mr. Bennet | 84.691% |
| Jane | Mr. Bennet | 84.691% |
| Charlotte | Mr. Lucas | 84.691% |
| Charlotte | Mrs. Bennet | 3.200% |
| Jane | Mr. Lucas | 6.111% |
| Mrs. Bennet | Mr. Bennet | 6.111% |
| Jane | Elizabeth | 3.200% |